Theoretischer Hintergrund

Für die Codierung der RDS Daten ist ein gekürzter "zyklischer" Code spezifiziert, der sowohl eine Blocksynchronisierung (Teilprojekt 5) als auch eine Fehlerkorrektur erlaubt.

Encodierung

Jeder Block besteht aus 16 Informationsbits:
Polynomschreibweise:

Die Encodierung der 16 Informationsbits erfolgt mittels des Generatorpolynoms

Hieraus läßt sich mittels modulo2 - Arithmetik das Codewort berechnen.

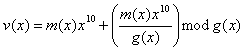
Mit Hilfe dieser Formel entsteht ein gekürzter systematischer (26,16) Code.
Dieser kann als folgende Schieberegisterschaltung implementiert werden:

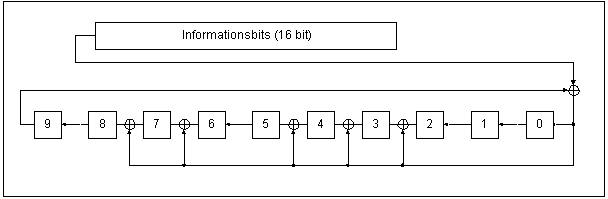
Nachdem die 16 Informationsbits in das Schieberegister hineingeschoben werden stehen die Prüfbits im Schieberegister. Mit der Matlabfunktion encodpoly.m kann diese Funktionalität simuliert werden.

Decodierung

Im Empfänger werden dann die durch die Encodierung hinzugefügten Prüfbits benutzt, um Fehler zu erkennen. Um die zu übertragene Bits möglichst kurz zu machen wurde ein gekürzter Code verwendet. Aus dem zyklischen (n =341, k = 331)Code wurde der gekürzte nichtzyklische (n-l = 26, k-l = 16) Code erzeugt (der Code wird so um l = 315 Stellen gekürzt). Diese Kürzung kann mittels Vormultiplikation des Empfangswortes rückgängig gemacht werden. Das Multiplikationspolynom kann mittels der Formel:

errechnet werden.
Das Syndrom kann dann wie bei zyklischen Codes durch das Prüfpolynom abgeleitet werden

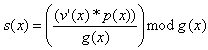
Auch dieser Algorithmus kann mit Schieberegistern technisch umgesetzt werden:

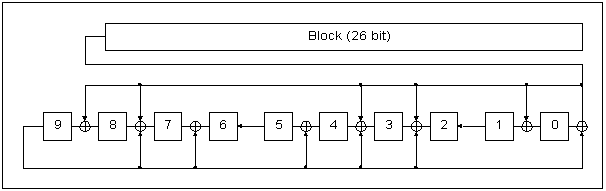
Wobei der Block v'(x) nach 26 Schritten im Schieberegister das Syndrom s(x) generiert. Die Abzapfungen oberhalb des Schieberegisters ist die Vormultiplikation (FIR-Filter), die Abzapfungen unterhalb die Polynomdivision das das Prüfpolynom (IIR-Filter).
Das Syndrom zeigt nun das Auftreten von Fehlern an. Falls das Syndrom ungleich 0 ist, sind Fehler aufgetreten und sie Fehlerkorrektur mittels Errortrapping folgt Die entspechend Matlabfunktion findet sich unter decodpoly.m.

Errortrapping

Durch die Anwendung des Errortrappingverfahren ist es hier möglich:
1) Alle Einzel- und Zweifachfehler in einen Block zu erkennen.
2) Alle Bündelfehler bis zur Länge von 10 Fehlern zu erkennen.
3) Bündelfehler der Länge 11 mit 99,9% Wahrscheinlichkeit zu erkennen
4) Bündelfehler der Länge größer 11 mit 99% Wahrscheinlichkeit zu erkennen.
Voraussetzung für die Anwendung ist, daß dieser Code die Korrektur von Bündelfehler bis zur Länge t = n-k = 5 erlaubt.
Grundlage der Errortrappingverfahrens ist die Tatsache, daß ein verschobener Empfangsvektor v' ein verschobenes Syndrom s erzeugt. Die Implementierung erfolgt wiederum durch eine Schieberegisterschaltung.

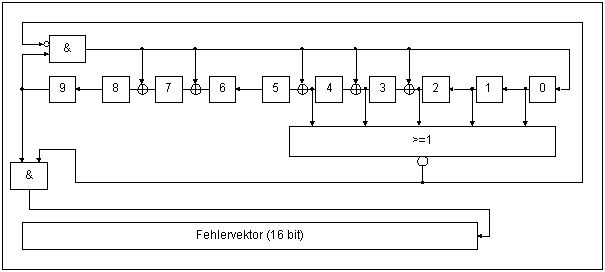
Das Syndrom s (Schieberegister) wird nun solange Verschoben bis das Errortrappingfomat auftritt (d.h. Bits 0-4 des Schieberegisters sind 0) oder nach 16 Verschiebungen die Unkorrigierbarkeit festgestellt wird.
Nach Auftreten der Errortrappingformats wird der Fehlervektor beschrieben, welcher dann auf den Informationteil des Empfangsvektors addiert wird (Modulo 2 Arithmetik!).
Auch das Errortrappingverfahren wurde mit Matlab simuliert (errortrapping.m).

Güte des Fehlerdekodierverfahrens

Um die Qualität dieser Kanalcodierung wurde mit Matlab getestet.
Nach der Encodierung eines Blockes (gültiges Codewort) wird ein Fehlervektor aufaddiert. Der Fehlervektor wird mittels der Zufallsfunktion in Matlab gemäß Gauß erzeugt. Somit kann gaußsches Rauschen auf den Übertragungsweg nachgebildet werden (jedoch keine Bursts).
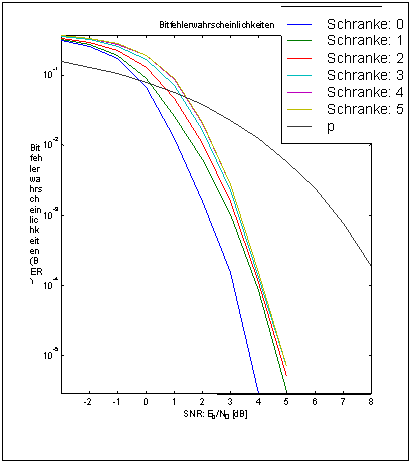
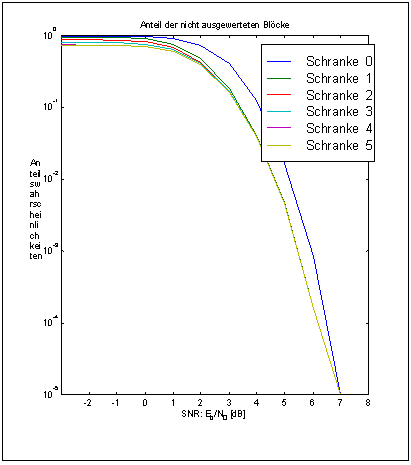
Nach der Decodierung und der Fehlerkorrektur wurde dann das ursprüngliche Nachrichtenwort und die empfangen Nachricht verglichen und ausgewertet. Die Fehlerrate wurde dann für verschiedene Einstellungen des Decoders über den SNR (signal noise ratio Signal-/Rauschverhältnis) aufgetragen. Im zweiten Graphen wurden demgegenübergestellt die Rate der übernommenen Blöcke.
Da diese Simulation ziemlich zeitaufwendig ist, konnten SNR bis 5dB errechnet werden.
Bei der Auswertung der Graphen man deutlichen den Codierungsgewinn zwischen unkorrigierten und korrigierten Nachrichten feststellen (ab 2dB SNR). Die Errortrappingdecodierung bietet noch die Einstellmöglichkeit die Fehleranzahl pro Block auszuwerten und dann einen Schwellwert festzulegen, unter welchen noch korrigiert wird. So kann man auf die Korrektur von 5 Bit Bündelfehler beispielsweise verzichten. Wertet man die Graphen nach diesen Gesichtspunkt aus, scheint ein Schwellwert (= maximaler Fehlerwert pro Block) von 1 sinnvoll, da bei ähnlicher Blockwegwerfrate der Codierungsgewinn ziemlich groß ist.
Die Simulation erfolgte mittels der Matlabfunktion testerror.m.