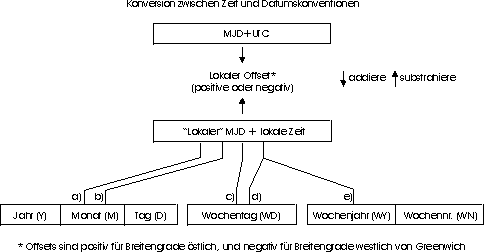
a) Berechnung von Y, M, D aus MJD
Y' = int [ (MJD - 15078,2) / 365,25 ]
M' = int { [ MJD - 14956,1 - int (Y' x 365,25) ] / 30,6001 }
D = MJD - 14956 - int ( Y' x 365,25 ) - int (M' x 30,6001 )
If M' = 14 or M' = 15, then K = l; else K = 0
Y = Y' + K
M=M'-l-Kxl2

b) Berechnung von MJD aus Y, M, D
If M = l or M = 2, then L = l; else L = 0
MJD = 14 956 + D + int [(Y - L) x 365,25] + int [(M + l + L x 12) x 30,6001]

c) Berechnung von WD aus MJD
WD = [ (MJD + 2) mod 7 ] + l

d) Berechnung von MJD aus WY, WN, WD
MJD = 15 012 + WD + 7 x { WN + int [ (WY x l 461 / 28) + 0,41] }

e) Berechnung von WY, WN aus MJD
W = int [ (MJD / 7) - 2 144,64 ]
WY = int [ (W x 28 / l 461) - 0,0079]
WN = W - int [ (WY x l 461 / 28) + 0,41]

Abkürzungen:
MJD	Modified Julian Day
UTC	Coordinated Universal Time
Y	Jahr von 1900 (z.B. für 2003, Y = 103)
M	Monat von Januar(= l) bis Dezember (= 12)
D	Tag des Monats von l bis 31
WY	"Wochennummer" Jahr von 1900
WN	Wochennummer gemäß ISO 2015
WD	Tag der Woche von Montag(= l) bis Sonntag (= 7)
K, L, M', W, Y'	temporäre Variablen
x	Multiplikation
int	Integer Anteil, ignoriert Nachkommastelle
mod 7	Modulo, bildet ganzzahligen Rest (0-6) nach Division durch 7